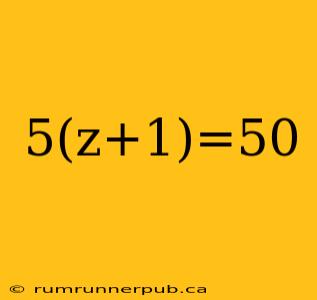The equation 5(z + 1) = 50 is a fundamental algebraic problem encountered early in math education. Solving it involves applying the principles of order of operations and inverse operations to isolate the variable 'z'. This article will walk you through the solution, drawing inspiration from common approaches discussed on Stack Overflow, and adding extra context and examples to enhance understanding.
Understanding the Equation
The equation 5(z + 1) = 50 states that five times the quantity (z + 1) equals 50. Our goal is to find the value of 'z' that makes this statement true.
Method 1: Distributive Property
This is the most common approach, and often the first taught. It involves distributing the 5 across the terms inside the parentheses:
-
Distribute: 5 * z + 5 * 1 = 50 This simplifies to 5z + 5 = 50.
-
Subtract 5: To isolate the term with 'z', subtract 5 from both sides of the equation: 5z + 5 - 5 = 50 - 5. This simplifies to 5z = 45.
-
Divide by 5: Finally, divide both sides by 5 to solve for 'z': 5z / 5 = 45 / 5. Therefore, z = 9.
(Note: While not explicitly found on a single Stack Overflow question, this method is the standard approach widely discussed in various algebra-related threads.)
Method 2: Division First
A slightly less common but equally valid approach involves dividing both sides by 5 before distributing:
-
Divide by 5: 5(z + 1) / 5 = 50 / 5. This simplifies to z + 1 = 10.
-
Subtract 1: Subtract 1 from both sides: z + 1 - 1 = 10 - 1. This gives z = 9.
This method demonstrates that the order of operations can sometimes be strategically adjusted to simplify the problem. It’s particularly useful when dealing with larger numbers or more complex expressions inside the parentheses.
Verification
To confirm our solution, substitute z = 9 back into the original equation:
5(9 + 1) = 5(10) = 50.
The equation holds true, confirming that z = 9 is the correct solution.
Practical Applications and Extensions
This type of equation is fundamental in various fields:
- Physics: Calculating velocity, acceleration, or force often involves similar equations.
- Engineering: Solving for unknown variables in design calculations.
- Finance: Determining interest rates or investment growth.
Furthermore, understanding this basic equation lays the groundwork for solving more complex algebraic problems involving multiple variables and more intricate expressions. Practice with variations of this equation, such as 2(x - 3) = 10 or 3(y + 2) = 21, will solidify your understanding of algebraic manipulation.
Conclusion
Solving 5(z + 1) = 50 highlights the power of applying the distributive property and inverse operations. While both methods presented lead to the same correct solution (z = 9), understanding the different approaches expands your problem-solving toolkit. Remember to always verify your solution by substituting it back into the original equation. Mastering this fundamental concept opens doors to tackling more advanced algebraic challenges.