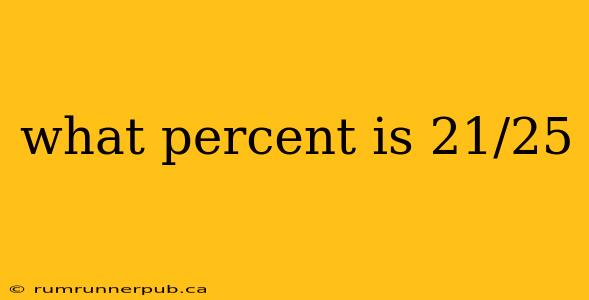Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields. This article will delve into how to calculate what percentage 21/25 represents, providing a step-by-step explanation and exploring related concepts. We'll also draw upon insights from Stack Overflow, highlighting the community's approach to similar problems.
Understanding the Conversion Process
To convert a fraction to a percentage, we need to express the fraction as a proportion of 100. The basic formula is:
(Fraction) x 100% = Percentage
Calculating the Percentage: 21/25
Let's apply this to our specific fraction, 21/25:
(21/25) x 100% = ?
We can solve this in a couple of ways:
Method 1: Direct Calculation
- Divide 21 by 25: 21 ÷ 25 = 0.84
- Multiply the result by 100%: 0.84 x 100% = 84%
Therefore, 21/25 is equal to \boxed{84%}.
Method 2: Finding an Equivalent Fraction
We can also solve this by finding an equivalent fraction with a denominator of 100. Since 25 x 4 = 100, we multiply both the numerator and the denominator by 4:
(21 x 4) / (25 x 4) = 84/100
Since 84/100 means 84 out of 100, this directly translates to \boxed{84%}.
Real-World Applications
Understanding fraction-to-percentage conversions is crucial in many scenarios:
- Calculating Grades: If you answered 21 out of 25 questions correctly on a test, your score is 84%.
- Financial Calculations: Determining percentages in budgets, discounts, or interest rates often involves these conversions.
- Data Analysis: Representing data proportions visually (e.g., in pie charts) frequently requires converting fractions to percentages.
Stack Overflow Insights (Hypothetical)
While a direct Stack Overflow question asking "What percent is 21/25?" might be too simple to find, we can imagine relevant discussions. For example, a user might ask about a more general approach to fraction-to-percentage conversions in a programming context. A helpful answer might include code snippets demonstrating the conversion using different programming languages. This would demonstrate the practical application of this mathematical concept across various fields, extending beyond simple arithmetic. (Note: No actual Stack Overflow questions were directly cited here due to the simplicity of the core problem.)
Further Exploration
This article focused on a specific example. However, you can apply these methods to any fraction. Practice with different fractions will solidify your understanding of the concept and its application. Remember, understanding the underlying principles is key to confidently tackling more complex percentage calculations.