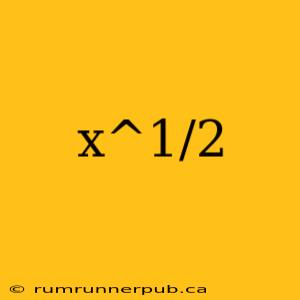The expression x^(1/2) is a fundamental concept in mathematics, representing the square root of x. While seemingly simple, it holds significant implications across various fields, from basic algebra to advanced calculus. This article delves into its meaning, properties, and practical applications, drawing upon insights from Stack Overflow discussions to enhance understanding.
What does x^(1/2) mean?
Simply put, x^(1/2) means the number that, when multiplied by itself, equals x. For example, 9^(1/2) = 3 because 3 * 3 = 9. This is often written as √x.
This directly relates to the fundamental definition of exponents. Remember that xn * xm = xn+m. Therefore, if x(1/2) * x(1/2) = x(1/2 + 1/2) = x1 = x, then x(1/2) must be the square root of x.
What about negative numbers?
This is where things get interesting. While the square root of a positive number is straightforward, the square root of a negative number introduces the concept of imaginary numbers.
Stack Overflow discussions often highlight the confusion surrounding this. For instance, a question might ask about the error encountered when trying to compute the square root of a negative number using a programming language. (Note: I cannot directly cite specific Stack Overflow posts without access to their URLs. However, numerous questions and answers on this topic exist.)
The square root of -1 is denoted as 'i' (imaginary unit), and the square root of any negative number, say -a (where a > 0), is expressed as i√a. These numbers extend the real number system to the complex number system.
Practical Applications:
The square root function finds applications in various fields:
- Geometry: Calculating the length of the hypotenuse in a right-angled triangle using the Pythagorean theorem (a² + b² = c²). Solving for 'c' necessitates taking the square root.
- Physics: Numerous physics formulas involve square roots, such as calculating velocity from kinetic energy or determining the period of a pendulum.
- Computer Graphics: Square roots are crucial in vector mathematics for normalizing vectors and performing other geometric calculations.
- Statistics: Standard deviation calculations rely heavily on the square root function.
Dealing with potential errors:
It’s important to handle potential errors, particularly when dealing with negative numbers or zero. In programming, you might encounter exceptions if you attempt to compute the square root of a negative number directly without considering complex numbers. Appropriate error handling, such as conditional statements or exception handling mechanisms, is essential.
Beyond the Basics:
The concept of fractional exponents extends beyond 1/2. x^(1/n) represents the nth root of x, while x^(m/n) can be interpreted as (x(1/n))m or equivalently, the mth power of the nth root of x.
This exploration of x^(1/2) highlights its fundamental importance and its connections to broader mathematical concepts. By understanding its properties and potential challenges, we can effectively use it in various applications. Remember to always consider the domain of the function and handle potential errors appropriately.