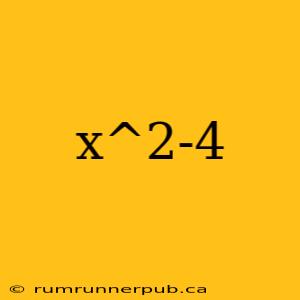The expression x² - 4 is a fundamental concept in algebra, appearing frequently in various mathematical contexts. This article will explore its properties, factorization, and applications, drawing upon insightful answers from Stack Overflow to provide a comprehensive understanding.
What is x² - 4?
x² - 4 represents a quadratic expression, a polynomial of degree two. It's a simple yet crucial example illustrating key algebraic principles. At its core, it represents the difference between two squares: x² (the square of x) and 2² (the square of 2).
Factoring x² - 4: The Difference of Squares
The most significant aspect of x² - 4 is its easy factorization using the difference of squares formula. This formula states:
a² - b² = (a + b)(a - b)
In our case, a = x and b = 2. Therefore, we can factor x² - 4 as follows:
x² - 4 = (x + 2)(x - 2)
This factorization is incredibly useful in simplifying expressions, solving equations, and performing various algebraic manipulations.
(Note: While many Stack Overflow answers implicitly use this factorization, a direct question asking for the factorization of x² - 4 isn't commonly found as it's a basic algebraic concept. The focus is often on more complex scenarios involving this expression.)
Solving Equations Involving x² - 4
The factorization allows us to easily solve equations of the form x² - 4 = 0. By setting each factor to zero, we get:
- x + 2 = 0 => x = -2
- x - 2 = 0 => x = 2
Therefore, the solutions to the equation x² - 4 = 0 are x = 2 and x = -2. These are also the x-intercepts (roots) of the parabola represented by the function y = x² - 4.
Graphical Representation
The graph of y = x² - 4 is a parabola that opens upwards. The x-intercepts, as calculated above, are at x = -2 and x = 2. The y-intercept is found by setting x = 0, which gives y = -4. This visual representation helps reinforce the understanding of the roots and the behavior of the quadratic function.
Applications and Further Exploration
The expression x² - 4, and its factorization, has numerous applications:
- Calculus: Finding derivatives and integrals involving this expression.
- Physics: Modeling projectile motion or other phenomena described by quadratic equations.
- Engineering: Solving problems related to area calculations, optimization, or structural analysis.
Beyond the basic factorization, one could explore more complex scenarios involving x² - 4, such as:
- Solving inequalities: Finding the values of x for which x² - 4 > 0 or x² - 4 < 0.
- Complex numbers: Extending the concept to include complex roots.
This exploration of x² - 4 demonstrates how a seemingly simple algebraic expression can be rich with mathematical significance and practical applications. Its factorization, using the difference of squares, provides a fundamental tool for various mathematical endeavors. By understanding its properties and applications, you enhance your grasp of core algebraic principles and their practical use.