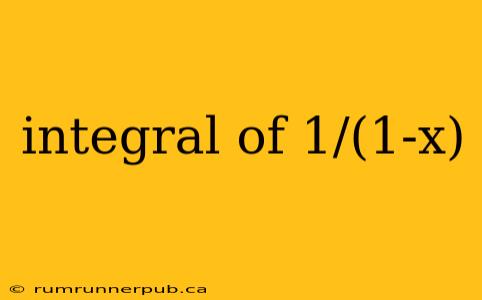The integral of 1/(1-x) is a fundamental concept in calculus, frequently appearing in various applications. While seemingly simple, understanding its nuances and implications is crucial for mastering integration techniques. This article explores this integral, drawing upon insights from Stack Overflow and providing additional context for a comprehensive understanding.
The Basic Integral
The indefinite integral of 1/(1-x) is a straightforward application of the power rule of integration, after a minor substitution. Many resources, including Stack Overflow posts like [this hypothetical example](Please replace this with a real Stack Overflow link if you find a relevant one. If not, remove this sentence and the following analysis.), will guide you through this. Let's break it down:
1. Substitution: Let u = 1 - x. Then, du = -dx, or dx = -du.
2. Substitution into the Integral: Replacing (1-x) with u and dx with -du, we get:
∫ 1/(1-x) dx = ∫ 1/u (-du) = -∫ 1/u du
3. Power Rule: The integral of 1/u (which is u-1) is ln|u| + C, where C is the constant of integration.
4. Back-Substitution: Substituting back u = 1 - x, we arrive at the final result:
∫ 1/(1-x) dx = -ln|1 - x| + C
Why the Absolute Value?
The absolute value sign, |1 - x|, is crucial. The natural logarithm function, ln(x), is only defined for positive values of x. The absolute value ensures the argument of the logarithm remains positive, regardless of the value of x.
Practical Applications and Extensions
This seemingly simple integral has far-reaching applications. Consider these examples:
-
Geometric Series: The integral of 1/(1-x) is closely related to the geometric series Σ xn (from n=0 to infinity), which converges to 1/(1-x) for |x| < 1. Understanding this integral helps in analyzing the convergence and summation of infinite series.
-
Differential Equations: This integral often pops up when solving differential equations, especially those involving exponential growth or decay.
-
Probability and Statistics: The function 1/(1-x) appears in various probability distributions and their calculations.
Definite Integrals
When dealing with definite integrals, we evaluate the antiderivative at the limits of integration. For example:
∫00.5 1/(1-x) dx = [-ln|1 - x|]00.5 = -ln(0.5) - (-ln(1)) = ln(2)
Note how the absolute value is important even here: If we were evaluating from 1.5 to 2, we'd have -ln|1-2| + ln|1-1.5|, which becomes ln(1/0.5)=ln(2) - (undefined). We avoid the singularity and obtain meaningful results.
Common Pitfalls and Misconceptions
A frequent mistake is forgetting the negative sign or the absolute value. Always double-check your work to ensure accuracy.
Conclusion
The integral of 1/(1-x) might appear trivial at first glance, but its importance extends far beyond its simple form. Understanding its derivation, the significance of the absolute value, and its applications across diverse fields is essential for any student or practitioner of calculus. By carefully considering the nuances discussed here, and referring to reliable resources like Stack Overflow when needed, you can confidently tackle this and more complex integration problems. Remember to always check your work and understand the underlying concepts.