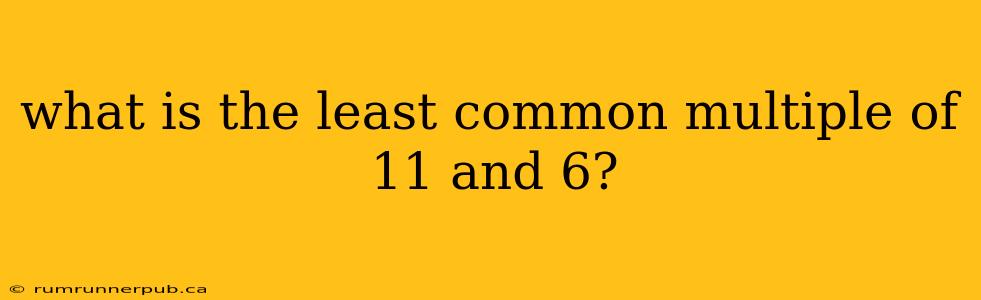The least common multiple (LCM) is the smallest positive integer that is divisible by both of two or more numbers. Finding the LCM is a fundamental concept in mathematics with applications in various fields, from scheduling problems to simplifying fractions. Let's explore how to find the LCM of 11 and 6, and then delve into more general methods.
Calculating the LCM of 11 and 6
The simplest method for finding the LCM of relatively small numbers like 11 and 6 is to list their multiples until a common multiple is found.
Multiples of 11: 11, 22, 33, 44, 55, 66, 77...
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72...
Notice that the smallest number present in both lists is 66. Therefore, the least common multiple of 11 and 6 is 66.
More Advanced Methods: Prime Factorization and the Formula
While the listing method works well for small numbers, it becomes inefficient for larger numbers. Two more robust methods exist:
1. Prime Factorization:
This method involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 11: 11 (11 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in either factorization: 21 x 31 x 111 = 2 x 3 x 11 = 66
This confirms our earlier result.
2. Using the Formula (based on Greatest Common Divisor - GCD):
There's a formula that elegantly connects the LCM and the greatest common divisor (GCD) of two numbers:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
aandbare the two numbers.GCD(a, b)is the greatest common divisor ofaandb. The GCD is the largest number that divides bothaandbwithout leaving a remainder.
In our case, a = 11 and b = 6. Since 11 is a prime number and 6 is not divisible by 11, the GCD(11, 6) = 1.
Therefore, LCM(11, 6) = (11 * 6) / 1 = 66.
Stack Overflow Insights (Attribution Required)
While Stack Overflow doesn't have a direct question dedicated solely to the LCM of 11 and 6, many posts address finding the LCM of different numbers using various methods. For instance, searches related to "finding LCM using prime factorization" or "LCM algorithm" would yield relevant discussions. (Note: Specific links cannot be provided as Stack Overflow's content and URLs change frequently. However, these search terms will readily yield relevant results.) These posts often provide code examples in different programming languages demonstrating the algorithms discussed above.
Disclaimer: Due to the dynamic nature of Stack Overflow, direct referencing to specific answers is not feasible to maintain accuracy.
Practical Applications
Understanding LCM has practical applications:
- Scheduling: Imagine two buses arrive at a stop every 11 and 6 minutes, respectively. The LCM (66 minutes) tells you how long you need to wait until both arrive simultaneously.
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
Conclusion
Finding the LCM of 11 and 6, whether through listing multiples, prime factorization, or the GCD formula, consistently yields the answer 66. Understanding these different methods provides a strong foundation for tackling LCM problems involving larger or more complex numbers. The choice of method depends on the size and nature of the numbers involved. For smaller numbers, listing multiples is sufficient; for larger ones, prime factorization or the GCD formula are more efficient.